IP Addressing and Subnetting - Part I

In Chapter 5, “Fundamentals of IP,” you learned about the basic concepts and terminology relating to IP addressing. These concepts were introduced early in the book because your understanding of many basic networking concepts depends on a base knowledge of IP addressing.
In this chapter, you will learn about the concepts and mathematics that let you analyze IP addresses and subnets. IP addressing is the only major topic that happens to get coverage on both of the INTRO and ICND exams. To answer questions on either CCNA exam, you will need to discover the structure of IP addresses, list the addresses in the same subnet, list the other subnets of that same network, identify the numbers of hosts in a subnet, and identify other information about addresses and subnets. This chapter describes the math and processes used to answer these questions.
This chapter also happens to cover a few topics related IP address scalability issues related to Internet growth.

Foundation Topics

This chapter begins with a brief review of IP addressing and subnetting. Following that, the text takes a thorough look at several types of IP addressing questions and the math you can use to find the answers.

IP Addressing Review

Chapter 5 explained the concepts behind IP addressing; Class A, B, and C networks; and subnetting. Before looking at the math behind IP addressing, a quick review will be helpful.
Many different Class A, B, and C networks exist. Table 12-2 summarizes the possible network numbers, the total number of each type, and the number of hosts in each Class A, B, and C network.



Without subnetting, a different IP network must be used for each physical network. For example, Figure 12-1 shows three example IP addresses, each from a different network. One address is in a Class A network, one is in a Class B network, and one is in a Class C network.



By definition, an IP address that begins with 8 in the first octet is in a Class A network, so the network part of the address is the first byte, or first octet. An address that begins with 130 is in a Class B network; by definition, Class B addresses have a 2-byte network part, as shown. Finally, any address that begins with 199 is in a Class C network, which has a 3-byte network part. Also by definition, a Class A address has a 1-byte host part, Class B has a 2- byte host part, and Class C has a 1-byte host part.
Humans simply can remember the numbers in Table 12-2 and the concepts in Figure 12-1
and then quickly determine the network and host part of an IP address. Computers, however, use a mask to define the size of the network and host parts of an address. The logic behind the mask results in the same conventions of Class A, B, and C networks that you already know, but the computer can deal with it better as a binary math problem. The mask is a 32-bit binary number, usually written in dotted-decimal format. The purpose of the mask is to define the structure of an IP address. In short, the mask defines the size of the host parts of an IP address, representing the host part of the IP address with binary 0s in the mask. Class A mask has its
last 24 bits as binary 0, which means that the last three octets of the mask are 0s. Table 12-3 summarizes the default masks and reflects the sizes of the two parts of an IP address.



IP Subnetting

IP subnetting creates vastly larger numbers of smaller groups of IP addresses, compared with simply using Class A, B, and C conventions. The Class A, B, and C rules still exist—but now a single Class A, B, or C network can be subdivided into many smaller groups. Subnetting treats a subdivision of a single Class A, B, or C network as if it were a network itself. By doing so, a single Class A, B, or C network can be subdivided into many nonoverlapping subnets.
Figures 12-2 and 12-3 show the basic differences between a network that does not use subnetting and one that does use subneting. First, look at Figure 12-2, which uses six different IP networks.



The design in Figure 12-2 requires six groups, each of which is a Class B network. The four LANs each use a single Class B network. In other words, the LANs attached to Routers A, B, C, and D are each a separate network. Additionally, the two serial inte the point-to-point serial link between Routers C and D use the same network because these two interfaces are not separated by a router. Finally, the three router interfaces composing the Frame Relay network with Routers A, B, and C are not separated by an IP router and would compose the sixth network.
Other Frame Relay IP addressing options would require one or two more IP network numbers for this physical network. CAUTION As in Figure 12-2, the design in Figure 12-3 requires six groups. Unlike Figure 12-2, Figure 12-3 uses six subnets, each of which is a subnet of a single Class B network.



This design subnets Class B network 150.150.0.0. The IP network designer has chosen a mask of 255.255.255.0, the last octet of which implies 8 host bits. Because it is a Class B network, there are 16 network bits. Therefore, there are 8 subnet bits, which happen to be bits 17 through 24—in other words, the third octet
Note that the network part (the first two octets in this example) all begin with 150.150, meaning that each of the six subnets is a subnet of Class B network 150.150.0.0. When subnetting, a third part of an IP address appears in the middle of the address—namely, the subnet part of the address. This field is created by “stealing” or “borrowing” bits from the host part of the address. The size of the network part of the address never shrinks—in other words, Class A, B, and C rules still apply when defining the size of the network part of an address. However, the
host part of the address shrinks to make room for the subnet part of the address. Figure 12-4 shows the format of addresses when subnetting.



Analyzing and Interpreting IP Addresses and Subnets

No one reading this book should be shocked to hear that IP addressing is one of the most important topics on both exams. You need a comfortable, confident understanding of IP addressing and subnetting for success on any Cisco certification. You should be prepared to answer questions about the following:
■ An interpretation of an address
■ Its network number
■ Its subnet number
■ The other IP addresses in the same subnet
■ The broadcast address
The other subnets that could be used if the same mask were in use In other words, you had better know IP addressing and subnetting!
Besides just answering questions on the CCNA exams, network engineers need to understand subnetting very well to do their jobs. Engineers who work with multiple networks must decipher IP addresses quickly, without running off to use a subnet calculator tool. For example, someone with a problem might call and tell you his IP address. After finding out the mask that’s used, you do a show ip route command on a router, but that typically lists subnets—so you
need to be able to easily figure out the subnet of which the address is a member. And not all networks will be using nice, easy subnet masks. No matter how useful this book is in helping you with a real networking job, the primary goal of this book is to help you pass the exam. So, the rest of this chapter is geared toward helping you understand how to interpret and analyze IP addresses.

Math Operations Used to Answer Subnetting Questions

Computers, especially routers, do not think about IP addresses in terms of the conventions shown in Table 12-2. They think in terms of 32-bit binary numbers, which is fine because, technically, that’s what IP addresses really are. Also, computers use a mask to define the structure of these binary IP addresses. A full understanding of what that means is not too difficult. However, getting accustomed to doing the binary math in your head is challenging for most of us, particularly if you don’t do it every day.
In this section, you will read about two key math operations that will be used throughout the discussion of answering CCNA addressing and subnetting questions. One operation converts IP addresses from decimal to binary and then back to decimal. The other operation performs a binary math operation called a Boolean AND .

Converting IP Addresses from Decimal to Binary, and Back Again

If you already know how binary works, how binary-to-decimal and decimal-to-binary conversion works, and how to convert IP addresses from decimal to binary and back, skip to the next section, “The Boolean AND Operation.” IP addresses are 32-bit binary numbers, written as a series of decimal numbers, separated by periods. To examine an address in its true form, binary, you need to convert from decimal to binary. To put a 32-bit binary number in the decimal form that is needed when configuring a router, you need to convert the 32-bit number back to decimal, 8 bits
at a time.
One key to the conversion process for IP addresses is remembering these facts:
When converting from one format to the other, each decimal number represents 8 bits.
When converting from decimal to binary, each decimal number converts to an 8-bit number.
When converting from binary to decimal, each set of 8 consecutive bits converts to one decimal number.
Consider the conversion of IP address 150.150.2.1 to binary for a moment. The number 150, when converted to its 8-bit binary equivalent, is 10010110. How do you know that? For now, look in the conversion chart in Appendix B, “Binary to Decimal Conversion Chart. The next byte, another decimal 150, is converted to 10010110. The third byte, decimal 2, is converted to 00000010; finally, the fourth byte, decimal 1, is converted to 00000001. The combined series of 8-bit numbers is the 32-bit IP address—in this case, 10010110 10010110 00000010 00000001.
If you start with the binary version of the IP address, you first separate it into four sets of eight digits. Then you convert each set of eight binary digits to its decimal equivalent. For example, writing an IP address as follows is correct but not very useful: 10010110100101100000001000000001
To convert this number to a more conveneint decimal form, first separate it into four sets of eight digits: 10010110 10010110 00000010 00000001
Then look in the conversion chart in Appendix B and find that the first 8-bit number converts to 150, and so does the second set. The third set of 8 bits converts to 2, and the fourth converts to 1—giving you 150.150.2.1.
Using the chart in Appendix B makes this much easier—but you will not have the chart on the exam, of course! So you can do a couple of things. First, you can learn how to do the conversion. The book does not cover it, but a couple of web sites referenced at the end of this section can help.

The other alternative is to use the chart when studying, and study the examples that show you how to manipulate IP addresses and find the right answers to the test questions without doing any binary math. If that works for you, you actually do not need to be speedy and proficient at doing binary-to-decimal and decimal-to-binary conversions.
One last important fact : When subnetting, the subnet and host parts of the address might span only part of a byte of the IP address. But when converting from binary to decimal and decimal to binary, the rule of always converting an 8-bit binary number to a decimal number is always true.

However, when thinking about subnetting, you will need to ignore byte boundaries and think about IP addresses as 32-bit numbers without specific byte boundaries. But that is explained more later in the section titled ”Finding the Subnet Number.“
Interestingly, you should actually be prepared to do basic binary, decimal, and hexadecimal conversions if taking the INTRO exam. While the shortcuts that can help you perform subnetting quickly are still very valuable, make sure you can convert numbers between all three types. Some sites that might help you if you want more information are as follows:
o For basic information on base 10, base 2 (binary), and conversion practice, visit
www.ibilce.unesp.br/courseware/datas/numbers.htm#mark2.
o For a description of the conversion process, try doit.ort.org/course/inforep/135.htm.
o For another description of the conversion process, try www.goshen.edu/compsci/mis200/decbinary.htm.
o For some free video classes that cover binary, conversion, and subnetting, go to www.learntosubnet.com
The Boolean AND Operation George Boole, a mathemetician who lived in the 1800s, created a branch of mathematics that came to be called Boolean math, after the name of its creator. Boolean math has many applications in computing theory. In fact, you can find subnet numbers, given an IP address and subnet mask, but using a Boolean AND.
A Boolean AND is a math operation performed to a pair of one-digit binary numbers. The result is another one-digit binary number. The actual math is even simpler than those first two sentences!

The following list shows the four possible inputs to a Boolean AND and the result:

■ 0 AND 0 yields a 0.
■ 0 AND 1 yields a 0.
■ 1 AND 0 yields a 0.
■ 1 AND 1 yields a 1.
In other words, the input to the equation consists of two one-digit binary numbers, and the output of the equation is one single-digit binary number. The only time the result is a binary 1 is when both input numbers are also binary 1; otherwise, the result of a Boolean AND is a 0 .
You can perform a Boolean AND on longer binary numbers, but you are really just performing an AND on each pair of numbers. For instance, if you wanted to AND together two four-digit numbers 0110 and 0011, then you would perform an AND of the first digit of each number and write down the answer. Then you would perform an AND on the second digit of each number, and so on, through the four digits. Table 12-4 shows the general idea.



The table separates the four digits of each original number to make the point more obvious. Look at the column holding the first digit’s values. The first digit of the first number is 0, and the first digit of the second number is also 0. 0 AND 0 yields a binary 0, which is listed as the Boolean AND result in that same column. Similarly, the second digits of the two original numbers are 1 and 0, respectively, so the Boolean AND result in the second digit column shows a 0. For the third digit, the two original numbers’ third digits were 1 and 1, so the AND result this time
shows a binary 1. Finally, the fourth digits of the two original numbers were 0 and 1, so the Boolean AND result is 0 for that column in the table.
When you Boolean AND two longer binary numbers together, you actually perform what is called a bitwise Boolean AND . This term simply means that you do what the previous example showed: You AND together the first digits from each of the two original numbers, then the second digits, and then the third, and so on, until the each pair of single-digit binary numbers has been ANDed.
IP subnetting math frequently uses a Boolean AND between two 32-bit binary numbers. The actual operation works just like the example in Table 12-4, except that it is longer.
To discover the subnet number in which a particular IP address resides, you perform a bitwise AND between the IP address and the subnet mask. Humans sometimes can look at an IP address and mask in decimal and derive the subnet number, but routers and other computers use a Boolean AND between the IP address and the subnet mask to find the subnet number, so you should understand the process. In this chapter, you also will read about a process by which you can find the subnet number without using any binary conversion or Boolean ANDs.
An example of the derivation of a subnet number is shown in Table 12-5.
NOTE Appendix B has a binary-to-decimal conversion chart.



First, focus only on the third column of the table. The binary version of the IP address 150.150.2.1 is listed first. The next row shows the 32-binary version of the subnet mask (255.255.255.0). The last row shows the results of a bitwise AND of the two numbers—in other words, the first bit in each number is ANDed, then the second bit in each number, then the third pair, and so on, until all 32 bits in the first number have been ANDed with the bit in the same position in the second number.
The resulting 32-bit number is the subnet number in which 150.150.2.1 resides. All you have to do is convert the 32-bit number back to decimal, 8 bits at a time. So, the subnet number in this case is 150.150.2.0.
If you understand the basic idea but would like additional examples to make it more clear, read on. In the next section, you will use Boolean ANDs to answer basic questions about IP subnetting.
Also, on the CD, look for the chapter titled “Subnetting Practice: 25 Subnetting Questions,” where 25 IP addressing practice questions are available, each with the binary math worked out for performing the Boolean AND.

Prefix Notation

Finally, any Cisco-oriented IP addressing coverage would be incomplete without a discussion of prefix notation.
In this chapter, you will get more comfortable using subnet masks. The masks can be written in decimal form, or they can be written as a 32-bit binary number. However, there is a third alternative, called prefix notation, which allows a router to display mask information more succinctly.
To understand prefix notation, it is important to know that all subnet masks have some number of consecutive binary 1s, followed by binary 0s. In other words, a subnet mask cannot have 1s and 0s interspersed throughout the mask—the mask always has some number of binary 1s, followed only by binary 0s.
Prefix notation simply denotes the number of binary 1s in a mask, preceded by a /. In other words, for subnet mask 255.255.255.0, whose binary equivalent is 11111111 11111111 11111111 00000000, the equivalent prefix notation would be /24 because there are 24 consecutive binary 1s in the mask. When talking about subnets, you can say things like “That subnet uses a slash 24 prefix ” or “That subnet has a 24-bit prefix” instead of saying something like “That subnet uses a mask of 255.255.255.0.”
Prefix notation makes talking about subnet masks a little easier, and it makes the information displayed by the router a little briefer as well. For instance, just try saying “255.255.255.0” out loud a few times, and imagine that the network is down while you’re saying it, and you will hear the benefit.
Now that the basic math tools have been covered, the specifics on how to use them to find the right answers to subnetting questions are covered next.

How Many Hosts, and How Many Subnets?

You also should know how to figure out how many network, subnet, and host bits are used with that subnetting scheme. From those facts, you easily can figure out how many hosts exist in the subnet and how many subnets you can create in that network using that subnet mask.
You already have learned that Class A, B, and C networks have either 8, 16, or 24 bits in their network fields, respectively. Those rules do not change. You also already have read that, without subnetting, Class A, B, and C addresses have 24, 16, or 8 bits in their host fields, respectively. With subnetting, the network part of the address does not shrink or change, but the host field shrinks to make room for the subnet field. So, the key to answering these types of questions is to figure out how many host bits remain after applying subnetting, which then can tell you the size of the subnet field. The rest of the answers follow from those two facts.
The following facts tell you how to find the sizes of the network, subnet, and host parts of an IP address:
• The network part of the address always is defined by class rules.
• The host part of the address always is defined by the mask; binary 0s in the mask mean that the corresponding address bits are part of the host field.
• The subnet part of the address is what’s left over in the 32-bit address.
Table 12-6 lists these three key facts along with the first example. If you have forgotten the ranges of values in the first octet for addresses in Class A, B, and C networks, refer to Table 12-2 earlier in the chapter.



In this example, there are 8 network bits because the address is in a Class A network, 8.0.0.0.
There are 16 host bits because, when you convert 255.255.0.0 to binary, there are 16 binary 0s—the last 16 bits in the mask. (If you do not believe me, look at Appendix B, in the binary- to-decimal conversion chart. 255 decimal is eight binary 1s, and 0 decimal is eight binary 0s.) The size of the subnet part of the address is what’s left over, or 8 bits.
Two other examples with easy-to-convert masks might help your understanding. Consider address 130.4.102.1, with mask 255.255.255.0. First, 130.4.102.1 is in a Class B network, so there are 16 network bits. A subnet mask of 255.255.255.0 has only eight binary 0s, implying 8 host bits, which leaves 8 subnet bits in this case.
For another example, consider 199.1.1.100, with mask 255.255.255.0. In fact, this example does not even use subnetting. 199.1.1.100 is in a Class C network, which means that there are 24 network bits. The mask has eight binary 0s, yielding 8 host bits, with no bits remaining for the subnet part of the address. In fact, if you remembered that the default mask for Class C networks is 255.255.255.0, you might have realized already that no subnetting was being used in this example.
Most of us can calculate the number of host bits easily if the mask uses only decimal 255s and 0s because it is easy to remember that decimal 255 represents 8 binary 1s, and decimal 0 represents 8 binary 0s. So, for every decimal 0 in the mask, there are 8 host bits. However, when the mask uses other decimal values besides 0 and 255, deciphering the number of host bits is more difficult. Examining the subnet masks in binary helps overcome the challenge. Consider the following addresses and masks, along with the binary version of the masks, as shown in Table 12-7.



The number of host bits implied by a mask becomes more apparent after converting the mask to binary. In the first mask, 255.255.252.0, there are ten binary 0s, implying a 10-bit host field.
Because that mask is used with a Class B address (130.4.102.1), implying 16 network bits, there are 6 remaining subnet bits. In the second example, the mask has only five binary 0s, for 5 host bits. Because the mask is used with a Class C address, there are 24 network bits, leaving only 3 subnet bits. The process so far is straightforward:
• The class rules define the network part.
• The mask binary 0s define the host part.
• What’s left over defines the size of the subnet part.
The only big problem occurs when the mask is tricky, which is true in the last two examples. When the mask is tricky, you have two alternatives for deciding how many host bits are defined:
• Convert the mask to binary, using any method for conversion at your disposal, and count the number of zeros.
• Convert the mask to binary after memorizing the nine decimal and binary values in Table 12-8.

These are the only nine valid decimal values used in a subnet mask. Converting a mask to binary without having to convert from decimal to binary will be much faster.
Table 12-8 lists the only valid decimal values in a mask and their binary equivalents. Memorizing these values will help you convert masks from between their decimal and binary forms more quickly on the exam.



Without the use of a calculator, PC, or decimal-to-binary conversion chart, binary conversion of a subnet mask becomes easy after memorizing this chart. The binary equivalents of 255 and decimal 0 are obvious. The other seven values are not. But notice the values in succession: Each value has an additional binary 1 and one less binary 0. Each mask value, in succession, shows a mask value that reduces the number of host bits by 1 and adds 1 to the size of the subnet field. If you simply memorize each decimal value and its binary equivalent, converting masks from decimal to binary will be a breeze. In fact, you could sit down to take the exam, and before starting, go ahead and write down the information in the table so you could easily refer to it during the exam.
So far, the book has not told you how to answer a question like this:
Given an address and mask, how many subnets are there? And how many hosts are there in a single subnet?
Well, two simple formulas provide the answers, and the formulas are based on the information that you just learned how to derive:

Number of subnets = 2 number-of-subnet-bits – 2
Number of hosts per subnet = 2 number-of-host-bits – 2

The formulas calculate the number of things that can be numbered using a binary number and then subtract 2 for two special cases. IP addressing conventions define that two subnets per network should not be used and that two hosts per subnet should not be used.
One reserved subnet, the subnet that has all binary 0s in the subnet field, is called the zero subnet . The subnet with all binary 1s in the subnet field is called the broadcast subnet —and it also is reserved. (Well, in fact, you can use both these subnets on a Cisco router, but it is recommended that you avoid using them. On the exam, the “right” answer is that you do not use them—hence the “minus 2” part of the 2 number-of-subnet-bits – 2 formula.) In fact, the courses upon which CCNA is based now use the term discouraged instead of reserved , meaning that although
those two subnets can be used, you should avoid it.
IP addressing conventions also reserve two IP addresses per subnet: the first (all binary 0s in the host field) and last (all binary 1s in the host field) addresses. No tricks exist to make these two addresses usable—they are indeed always reserved.
Table 12-9 summarizes the five examples used so far in this chapter.



The details of the algorithm used to answer subnetting questions about the number of hosts and subnets are summarized in the following list:
Step 1 Identify the structure of the IP address.
Step 2 Identify the size of the network part of the address, based on Class A, B, and C rules.
Step 3 Identify the size of the host part of the address, based on the number of binary 0s in the mask. If the mask is tricky, use the chart of typical mask values to convert the mask to binary more quickly.
Step 4 The size of the subnet part is what’s “left over”; mathematically, it is 32 – (number of network + host bits).
Step 5 Declare the number of subnets, which is 2 number-of-subnet-bits – 2.
Step 6 Declare the number of hosts per subnet, which is 2 number-of-host-bits – 2.

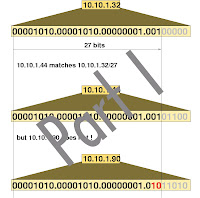
What Is the Subnet Number, and What Are the IP Addresses in the Subnet?

One of the most common things you need to figure out is that after you know an IP address and subnet mask, you must answer questions about them. The question might be straightforward, such as “What is the subnet number?”, or it might be more subtle, such as “Which of the following IP addresses are in the same subnet as the stated address?” In either case, if you can dissect an IP address as described in this chapter, you can answer any variation of this type of question.
In the next several sections, you will learn how to derive the subnet number and the subnet broadcast address. After deriving these two values, you easily can find the range of valid IP addresses in the subnet.

Finding the Subnet Number

Earlier, you learned that computers perform a Boolean AND of the address and mask to find the subnet number. The following tables (Tables 12-10 through 12-14) show the Boolean AND process for the five examples used in the previous section of this chapter:



Although the tables show the answers, they do not show the process. The steps taken to complete the tables are as follows:
Step 1 To begin, you start with a decimal address and mask stated in the question.
Step 2 Then you must convert the two numbers to binary, as seen in all five examples.
Step 3 Next, each bit is ANDed with the bit in the same position in the other number (in other words, a bitwise Boolean AND), giving the result of the Boolean AND.
Step 4 Finally, the Boolean AND result must be converted back to decimal.
The last step in this process, conversion of the binary number back to decimal, is the step that causes most of the problems for people new to subnetting. In some cases, the conversion is simple. For instance, in the first example, the subnet mask is 255.255.0.0. Because the mask has only 255s or 0s in decimal, the boundary between the subnet and host fields is on a byte boundary as well—between the second and third bytes, in this case. So, the conversion from binary back to decimal for the result of the Boolean AND—0000 1000 0000 0001 0000 0000 0000 0000—typically does
not pose a problem.
The confusing typically arises when the boundary between the subnet and host part of the address is in the middle of a byte, which occurs when the subnet mask has some value besides 0 or 255 decimal. For example, with 130.4.102.1, mask 255.255.252.0, the first 6 bits of the third octet comprise the subnet field, and the last 2 bits of the third octet, plus the entire fourth octet, comprise the host field. The problem that some people experience is that they try to convert the 6-bit subnet part from binary to decimal, and the 10-bit host part to decimal.
However, when converting binary to decimal to find the dotted decimal IP address, you always convert the entire octet—even if part of the octet is in the subnet part of the address and part is in the host part of the address.
So, in this example, the subnet number (130.4.100.0), in binary, is 1000 0010 0000 0100 0110 0100 0000 0000. The entire third octet is shown in bold, which converts to 100 in decimal. When converting, each set of 8 bits is converted to decimal, giving 130.4.100.0.

Finding the Subnet Broadcast Address

The subnet broadcast address, sometimes called the directed broadast address , can be used to send a packet to every device in a single subnet. However, few tools and protocols use the subnet broadcast address anymore. However, by calculating the subnet broadcast address, you easily can calculate the largest valid IP address in the subnet, which is an important part of answering subnetting questions.
There is a binary math operation to calculate the subnet broadcast address. However, there is a much easier process, especially if you already have the subnet number in binary:
Change all the host bit values in the subnet number to binary 1s.
You can examine this simple math behind calculating the subnet broadcast address in the five tables (Tables 12-15 through 12-19) that follow. The host parts of the addresses, masks, subnet numbers, and broadcast addresses are in bold.





Simply by examining the subnet broadcast addresses in binary, you can see that they are identical to the subnet numbers, except that all host bits have a value of binary 1 instead of binary 0.

(Look for the bold digits in the examples.)
For those of you who just want to know, to derive the broadcast address using Boolean math, first start with the subnet number and mask, in binary. Invert the mask (“invert” means change all 1s to 0s, and all 0s to 1s). Then do a bitwise Boolean OR between the two 32-bit numbers. (An OR yields a 0 when both bits are 0 and yields a 1 in any other case.) The result is the subnet broadcast address.
NOTE : For those of you who just want to know, to derive the broadcast address using Boolean math, first start with the subnet number and mask, in binary. Invert the mask (“invert” means change all 1s to 0s, and all 0s to 1s). Then do a bitwise Boolean OR between the two 32-bit numbers. (An OR yields a 0 when both bits are 0 and yields a 1 in any other case.) The result is the subnet broadcast address.

Finding the Range of Valid IP Addresses in a Subnet

You also need to be able to figure out which IP addresses are in a particular subnet and which are not. You already know how to do the hard part of finding that answer. You know that in any subnet, two numbers are reserved. The two reserved numbers are the subnet number itself and the subnet broadcast address. The subnet number is the numerically smallest number in the subnet, and the broadcast address is the numerically largest number. So, the range of valid IP addresses starts with one more than the subnet number and ends with the address that is one less than the broadcast address. It’s that simple!
A formal definition of the “algorithm” to find the first and last IP addresses in a subnet after the subnet number and broadcast addresses are known is as follows:
• For the first valid IP address: Copy the subnet number, but add 1 to the fourth octet.
• For the last valid IP address: Copy the subnet broadcast address, but subtract 1 from the fourth octet.
• The range of valid IP addresses starts with the first number and ends with the last. Tables 12-20 through 12-24 summarize the answers for the five examples used in this section.


IP Addressing and Subnetting - Part I





Continued to Part II

IP Addressing and Subnetting - Part I